这篇文章上次修改于 703 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
序列解题报告
建议到我的博客里食用
题意:
首先定义一个目标序列,称为 $k-$ 序列:对于序列中的每一项 $s$,序
列中至少有 $k-1$ 个其他项都等于 $s$。每次操作可以使序列中的任何一项的值减小 $1$。现在给定一个长度为 $n$ 的升序序列和 $k$,你的任务是帮OIER们计算出转化为 $k-$ 序列需要的最少步数
换句话来说这个序列中的任意一个数必须有至少 $k$ 个与他相同的数。
苦苦挣扎第一步:
瞄了一眼数据范围,$2 \leq k \leq n \leq 5*10^5$,应该只能是 $O(n)$ 或者 $O(nlogn)$ 之类的时间复杂度乱搞一下,反过来看一下题序列是已经排好序的,会不会有什么蹊跷呢?贪心?吧每$ k$ 个数字分到一组,通过减把他们全部变成一样的,不幸的是,这样的算法虽然优美,但是是不正确的。只能无奈放弃。
苦苦挣扎第二步:
关于处理序列上的算法无非几个,好像都不能用,只好乱搞一下DP了,因为数据范围巨大,只能开一维dp或者最多加一个 $log(n)$ ,这道题好像也没有要倍增之类的东西,先开成一维,最好想的应该就是前 $k$ 个数是 $k-$ 序列的,根据之前贪心的想法肯定是把数组弄成很多个长度大于等于 $k$ 的连续区间,dp就以当前这个点为后面这个区间的右端点,枚举左端点,动规方程显而易见:
$dp_i=dp_j+sum_i-sum_j-(i-j)*a_{j+1}$ $(k \leq i)$
$dp_i=inf$ $(i<k)$
苦苦挣扎第三步:
可惜这么好的DP却太慢的,时间复杂度直逼 $O(n^2)$,虽然常数较小,但是抵不住 $2 \leq k \leq n \leq 5*10^5$ , 优化!!!
之前的把 $O(n^2)$ DP优化成 $O(n)$ 需要使用单调队列,要求dp数组有单调性,这道题没有,不行,难道要放弃了吗,还有斜率优化!!!
拆拆大法好!!!:$dp_i=dp_j+sum_i-sum_j-i\times a_{j+1}+j \times a_{j+1}$
拆完之后再移一下项:$dp_i-sum_i+i\times a_{j+1}=dp_j-sum_j+j\times a_{j+1}$ $(k \leq i)$
成功地把与 $i$ 相关的,与 $j$ 相关的,与 $i,j$ 都相关的,分别移到一起,肯定有人问了:这么做干嘛呢,没关系只要这样看这个方程:
$(dp_i-sum_i)+(i)\times (a_{j+1})=(dp_j-sum_j+j\times a_{j+1})$ $(i>=k)$
一次函数!!!,平面直角坐标系中有很多与$j$相关的点,相当于过这些点做斜率为 $k$ 的直线交 $y$ 轴于一个点,这个点的纵坐标就是 $y$ ,而 $y$ 就相当于 $dp_j$ 加上很多与 $i$ 相关的常数,因为我们在枚举 $i$ ,所以这些常数是可以确定的,不与 $j$ 相关,接下来就是要求这些交点的纵坐标的最小值。可是怎么优化到 $O(1)$ 求呢,不要慌,慢慢来。
再套一层单调队列,在理解为什么是这样之前先来看看这些点:
样例太小了换一个:
9 2
1 2 8 9 15 16 16 16 20结合样例来看当 $i=9$ 是,应该有决策点 $7,6,5,4,3,2,1,0$ ,画上坐标轴。(下面有图)
$0,1$ 是 $inf$ , 所以没画
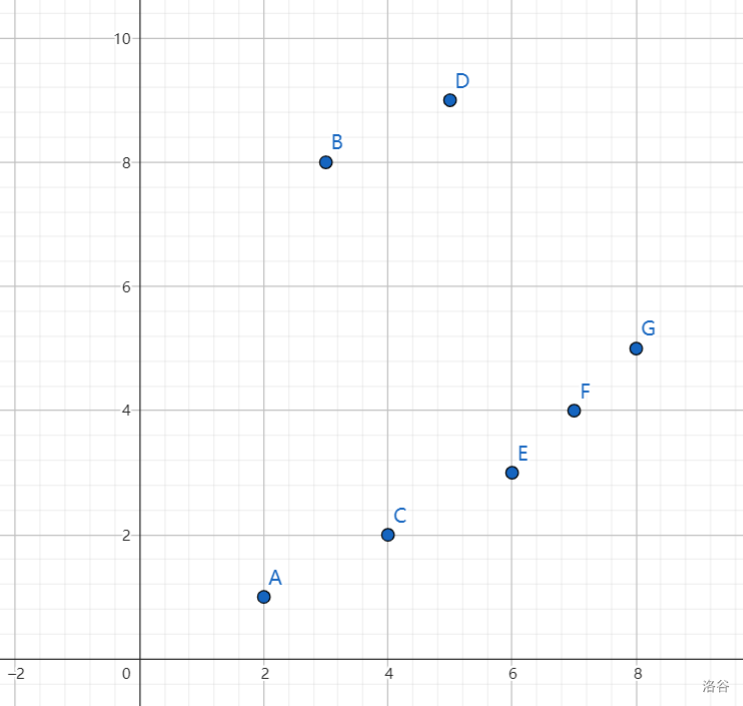
维护一个有序点集,使得这个点集相邻的两个点相连所得的直线斜率单调递增,这个就是用单调队列优化
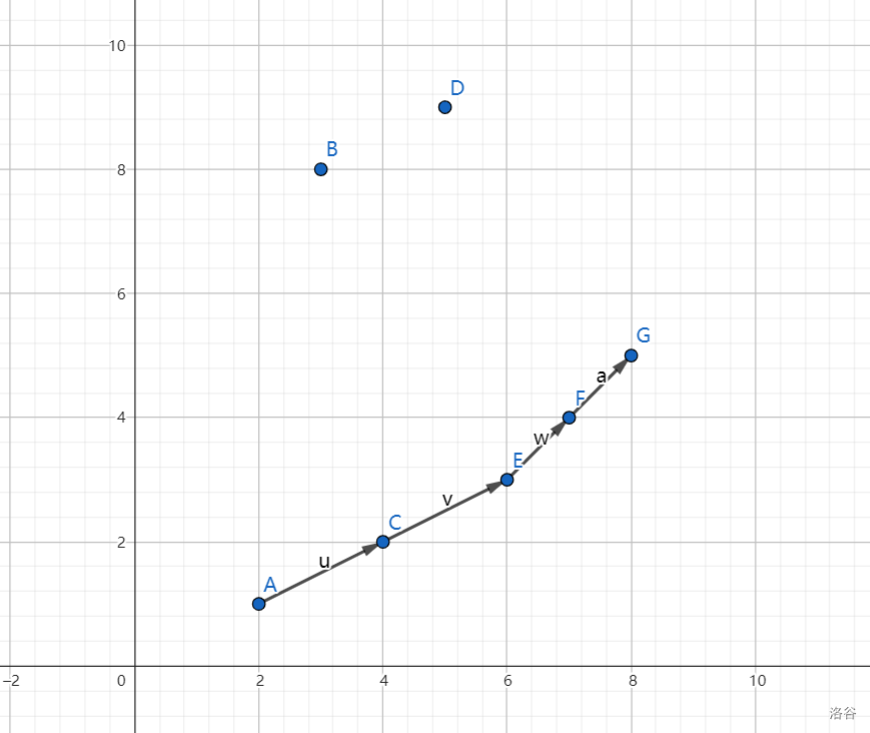
数据没出好,按理说是 $n$ 条线段头尾相接。
显然的,我们会让相连斜率小于上面 $(dp_i-sum_i)+(i)\times (a[j+1])=(dp_j-sum_j+j\times a_{j+1})$ $(i>=k)$ 方程中的 $k$ 也就是 $i$ 弹出,因为 $i$ 单调递增,所以后面也不会考虑他,因为 $b=y-kx$ ,斜率太小的话, $x$ 肯定会很小, $b$ 就更大了,很显然把这些点去掉之后,
就选的是最下面那个点,再往上走斜率越大,$y$ 增长得很快,也不满足最小。
仍然有个小问题,在计算斜率的时候,double不靠谱,根据等式的性质2,转换乘为除:
$(y_1-y_2)/(x_1-x_2)<(y_3-y_4)/(x_3-x_4)$
等同于
$(y_1-y_2)\times (x_3-x_4)<(y_3-y_4)\times (x_1-x_2)$
代码就很好写了,注意一个 $x$ 对应多个 $y$ 的情况,这种情况斜率处理成无限大。
#include <iostream>
#include <cstdio>
#include <cstring>
#define int long long
inline int read();
int a[500005];
int l,r;
int sum[500005];
int que[500005];
int dp[500005];
double y(int r){
return dp[r]-sum[r]+r*a[r+1];
}
double x(int r){
return a[r+1];
}
signed main(){
#ifdef ONLINE_JUDGE=LUOGU
#else
freopen("sequence.in","r",stdin);
freopen("sequence.out","w",stdout);
#endif
memset(a,0,sizeof(a));
memset(sum,0,sizeof(sum));
memset(dp,0,sizeof(dp));
memset(que,0,sizeof(que));
l=r=0;
int n=read(),k=read();
for(int i=1;i<=n;i++){
a[i]=read();
sum[i]=a[i]+sum[i-1];
}
// que[0]=-1;
for(int i=1;i<=n;i++){
if(i-k>=k){
while(l<r&&(y(que[r])-y(que[r-1]))*(x(i-k)-x(que[r]))>=(y(i-k)-y(que[r]))*(x(que[r])-x(que[r-1]))){
r--;
}
que[++r]=i-k;
}
while(l<r&&y(que[l+1])-y(que[l])<=(i)*(((x(que[l+1])-x(que[l]))))){
l++;
}
int j=que[l];
if(i-k<0){
dp[i]=0x3f3f3f3f3f3f3f3f;
}else if(j!=-1){
dp[i]=dp[j]+(sum[i]-sum[j])-(i-j)*a[j+1];
}else
dp[i]=(sum[i])-(i-j)*a[j+1];
}
printf("%lld\n",dp[n]);
return 0;
}
inline int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){
c=='-'?f=-1:1;
c=getchar();
}
while(c>='0'&&c<='9'){
x=(x<<3)+(x<<1)+(c^48);
c=getchar();
}
return f*x;
}
/*
Anything about this program:
Type:
Description:
Example:
1:
In:
Out:
More:
*/
作者懒癌晚期,前两个非正解不想写代码了,希望各位理解
POJ3709是这道题的加强版,多了个多组数据,可以去A一下